语言特性
- Python是静态还是动态类型?是强类型还是弱类型?
- 动态强类型语言
- 动态还是静态指的是在编译期还是运行期确定类型
- 强类型指的是不会发生隐式类型转换
- Python作为后端语言优缺点
- 胶水语言,轮子多,应用广泛
- 语言灵活,生产力高
- 性能问题,代码维护,python2/3版本兼容问题
-
鸭子类型
- 关注点在对象的行为,而不是类型
- monkey patch
- 所谓的monkey patch就是运行时替换
- 比如gevent库需要修改内置的socket
1 2
from gevent import monkey monkey.patch_socket()
-
自省(Introspection)
- 运行时判断一个对象的类型的能力
- Python一切皆对象,用type,id,isinstance获取对象类型信息
- Inspect模块提供更多获取对象信息的函数
-
列表推导
1
[i for i in range(10) if i %2 == 0]
-
字典推导
1 2 3 4
a = ['a', 'b'] b = [1, 2] d = {k:v for k,v in zip(a,b)} # d = {'a': 1, 'b':2}
Python2/3差异
Python3改进
- 编码,Python3默认str是unicode,不再有Unicode对象
- print成为函数
- 除法,Python3除号返回浮点数,Python2是整数
- 类型注解(type hint),帮助IDE实现类型检查
- 优化的super()方便直接调用父类函数
- 高级解包操作,a, b , *c = range(10)
- 限定关键字参数
- Python3重新跑出异常不会丢失栈信息
- 一切返回迭代器(range,zip, map,etc)
- yield from 链接子生成器
- asyncio内置库,async/await原生协程支持异步编程
- 新的内置库(enum,mock,asynio,concurrent.futures,etc)
- 生成的pyc文件统一放到
__pycache__ - 一些内置库的修改(urllib,selector,etc)
- 性能优化等
兼容Python2/3的工具
- six模块
- 2to3等工具转换代码
__future__模块
Python如何传递参数
函数传参
- 值传递还是值引用?唯一支持的参数传递是共享传参
- Call by Object(Call by Object Reference or Call by Sharing)
- 共享传参,函数形参获得实参中各个引用的副本
Python可变/不可变对象
- 不可变对象(bool/int/float/tuple/str/frozenset)
- 可变对象(list/set/dict)
*args, **kwargs
- 用来处理可变参数
- *args被打包成tuple
- **kwargs被打包成dict
Python异常处理
什么时候需要捕获处理异常
- 网络请求(超时、连接错误等)
- 资源访问(权限问题、资源不存在等)
- 代码逻辑(越界访问、KeyError等)
1
2
3
4
5
6
7
8
try:
# 可能会抛出异常的代码
except (Exception1, Exception2) as e:
# 异常处理代码
else:
# 异常没有发生时的代码逻辑
finally:
# 无论是否有异常,都会执行的代码
如何自定义异常
- 继承Exception实现自定义异常
- 给异常加上一些附加信息
- 处理一些业务相关的特定异常
Python性能分析与优化
什么是Cpython GIL(Global Interpreter Lock)
- Cpython解释器的内存管理不是线程安全的
- 保护多线程情况下对Python对象的访问,Cpython使用粗粒度的锁机制避免多个线程同时执行字节码
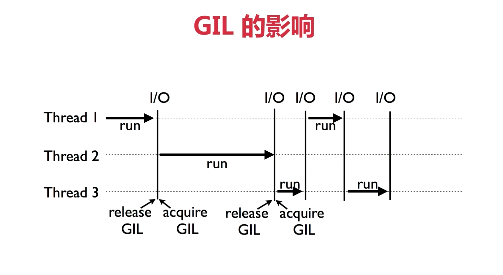
GIL的影响
- 限制了程序的多核执行
- 同一时间只能有一个线程执行字节码
- CPU密集程序难以利用多核优势
- IO密集程序影响不大,在IO期间会释放GIL
如何规避GIL影响
- CPU密集可以使用多进程+进程池
- IO密集使用多线程/协程
- cython扩展
为什么有了GIL还要关注线程安全
- 一个操作如果是一个字节码指令可以完成的就是原子的
- 原子的可以保证线程安全的
- 使用dis操作来分析字节码
如何剖析程序性能
- 二八定律,大部分时间耗时在少量代码上
- 使用profile或cprofile等内置工具
- 使用pyflame等工具
服务端性能优化措施
- web应用,一般语言不会成为瓶颈
- 数据结构和算法优化
- 数据库层:索引优化,慢查询消除,批量操作减少IO,NoSQL
- 网络IO:批量操作,pipeline操作减少IO
- 缓存:使用内存数据库,redis或memcached
- 异步:asyncio,celery
- 并发:gevent,多线程
- 并行:多进程
Python生成器与协程
什么是生成器
- 生成器就是可以生成值的函数
- 当一个函数里有了yield关键字就是生成器
- 生成器可以挂起执行并且保持当前执行的状态
基于生成器的协程(Generator Based Coroutine)
- Python3之前没有原生协程,只有基于生成器的协程
- 生成器可以通过yield暂停执行和产出数据
- 同时支持send()向生成器发送数据和throw()向生成器抛出异常
协程注意点
- 协程需要使用send()或者next(coroutine)来primer(预激)才能启动
- 在yield处协程会暂停执行
- 单独的yield value会产出值给调用方
- 可以通过coroutine.send(value)来给协程发送值,发送的值会赋值给yield表达式左边的变量value = yield
- 协会执行完成后(没有下一个yield语句)会抛出StopIteration异常
协程装饰器
避免每次都要使用send来预激
1
2
3
4
5
6
7
8
9
10
from functools import wraps
def coroutine(func):
"""装饰器 向前执行到第一个yield表达式预激func"""
@wraps(func)
def primer(*args, **kwargs):
gen = func(*args, **kwargs)
next(gen)
return gen
return primer
Python3原生协程
- Python3.5引入async/await支持原生协程(native coroutine)
单元测试
什么是单元测试
- 针对程序模块进行正确性检验
- 一个函数,一个类型进行验证
- 自底向上保证程序正确性
为什么要写单元测试
- 保证代码逻辑的正确性,甚至有些公司采用测试驱动开发(TDD)
- 单元测试影响设计,易测的代码往往是高内聚低耦合的
- 回归测试,防止改一处代码,整个服务不可用
单元测试相关库
-
nose/pytest/unittest
- mock模块用来模拟替换网络请求等
- coverage统计测试覆盖率
内置数据结构和算法
| 数据结构/算法 | 语言内置 | 内置库 |
|---|---|---|
| 线性结构 | list/tuple | array/collections.nametuple |
| 链式结构 | collections.deque | |
| 字典结构 | dict | collections.Counter/OrderedDict |
| 集合结构 | set/frozenset | |
| 排序算法 | sorted | |
| 二分算法 | bisect | |
| 堆算法 | heapq | |
| 缓存算法 | functools.lru_cache(python3) |
Python dict底层数据结构
- 为了支持快速查找使用了哈希表作为底层结构
- 哈希表平均查找时间复杂度O(1)
- CPython解释器使用二次探查解决哈希冲突问题
Python list/tuple区别
- 都是线性结构,支持下标访问
- list是可变对象,tuple保存的引用不可变
- list没法作为字典的key,tuple可以(可变对象不可hash)
排序算法
| 排序算法 | 最差时间分析 | 平均时间复杂度 | 稳定度 | 空间复杂度 |
|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n^2) | 稳定 | O(1) |
| 选择排序 | O(n^2) | O(n^2) | 不稳定 | O(1) |
| 插入排序 | O(n^2) | O(n^2) | 稳定 | O(1) |
| 快速排序 | O(n^2) | O(n*log2n) | 不稳定 | O(log2n)~O(n) |
| 堆排序 | O(n*log2n) | O(n*log2n) | 不稳定 | O(1) |